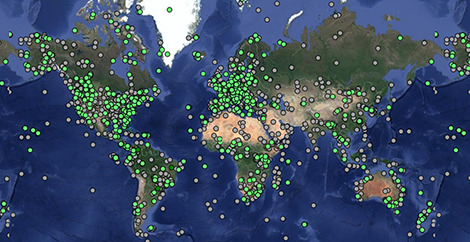
Tracking data
Explore animal movements on our interactive map.
Get started
Are you a researcher, journalist, student or developer? Whether you want to explore what’s here, add your data, or initiate a new project, get headed in the right direction.
News
Updates to improve account management
Dear Movebank users,
We have improved the Movebank login procedure and the account managment. Continue reading...
About us
Movebank is a free, online database of animal tracking data hosted by the Max Planck Institute of Animal Behavior. We help animal tracking researchers to manage, share, protect, analyze and archive their data.
- 6.3 billion locations
- 6.9 billion other sensor records
- 8,242 studies
- 1,400 taxa
- 4,180 data owners